无论是在机器学习,深度学习还是人工智能中,我们都在寻找一种模拟人脑的机制,注意力机制源于人脑,比如当我们欣赏一本书的时候,当我们对某个知识点感兴趣的时候,会映像深刻,可能会反复读某一段文字,但是对于其他不敢兴趣的内容会忽略,说明人脑在处理信号的时候是一定会划权重,而注意力机制正是模仿大脑这种核心的功能。
本文为了介绍注意力机制,参考《动手学深度学习》的注意力机制部分。
1、什么是注意力机制
在卷积,全连接等神经网络中,都只考虑不随意的线索,只关注重要的特征信息。 注意力机制是考虑所有线索,并关注其中最重要的特征信息:
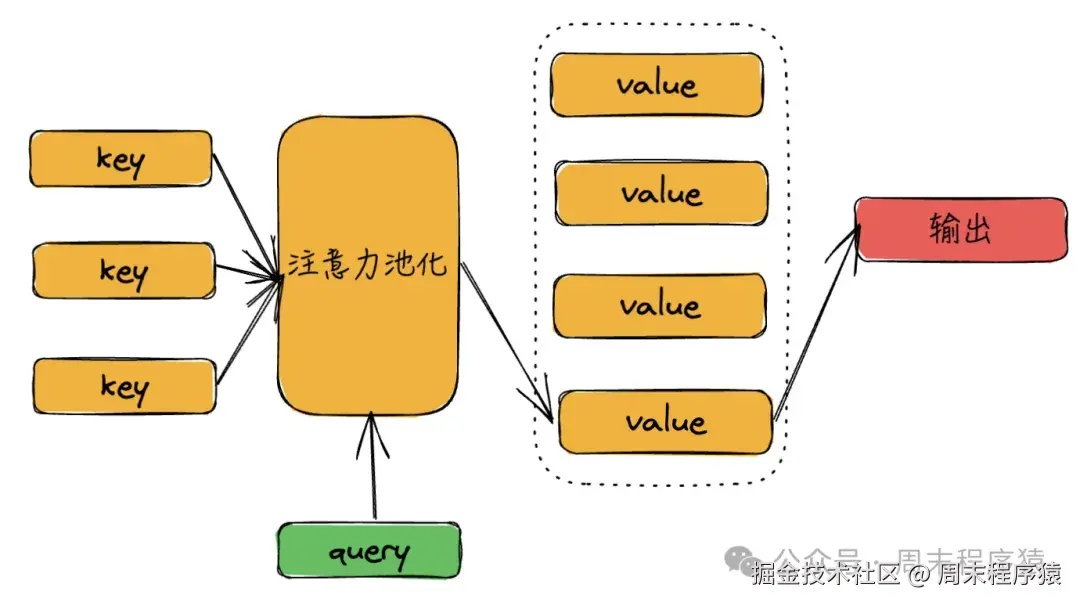
(1)非参数注意力
非参数注意力机制是使用查询和键值对来计算注意力权重,然后通过加权平均来获得输出,数学表达式:
其曲线如下:
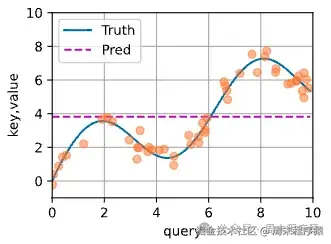
可以认为x=query,y=key=value,其中输入任何一个x,输出都是平均值,但是这个函数的设计不太合理,因此Nadarrya和Watson提出更好的想法,其公式如下:
通过核函数将x和xi的距离关系做映射,如果一个xi(key)越接近给定的查询x,那么给yi(value)的权重就越大,反之越小,这样就可以控制注意力的大小,其曲线如下:
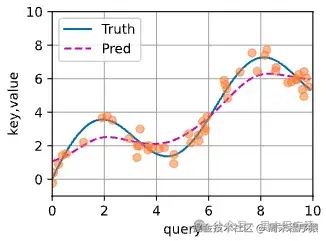
两段验证的代码也给出来(参考《动手学深度学习》):
import torch
from torch import nn
n_train = 50 # 训练样本数
test_len = 10
x_train, _ = torch.sort(torch.rand(n_train) * test_len) # 排序后的训练样本
def f(x):
return 2 * torch.sin(x) + x**0.8
y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,)) # 训练样本的输出
x_test = torch.arange(0, test_len, 0.1) # 测试样本
y_truth = f(x_test) # 测试样本的真实输出
n_test = len(x_test) # 测试样本数
n_test
# 求平均值
y_hat = torch.repeat_interleave(y_train.mean(), n_test)
print(y_hat)
X_repeat = x_test.repeat_interleave(n_train).reshape((-1, n_train))
attention_weights = nn.functional.softmax(-(X_repeat - x_train)**2 / 2, dim=1)
y_hat = torch.matmul(attention_weights, y_train)
(2)参数注意力
非参数和参数的区别在于,参数注意力使用的是参数矩阵,而非参数注意力使用的是核函数,其公式如下:
参数矩阵需要学习一个w参数,通过w参数拿到最优的拟合曲线,最简单的方法就是通过训练,训练代码如下(参考《动手学深度学习》):
class NWKernelRegression(nn.Module):
def __init__(self, **kwargs):
super().__init__(**kwargs)
self.w = nn.Parameter(torch.rand((1,), requires_grad=True))
def forward(self, queries, keys, values):
# queries和attention_weights的形状为(查询个数,“键-值”对个数)
queries = queries.repeat_interleave(keys.shape[1]).reshape((-1, keys.shape[1]))
self.attention_weights = nn.functional.softmax(
-((queries - keys) * self.w)**2 / 2, dim=1)
# values的形状为(查询个数,“键-值”对个数)
return torch.bmm(self.attention_weights.unsqueeze(1),
values.unsqueeze(-1)).reshape(-1)
X_tile = x_train.repeat((n_train, 1))
Y_tile = y_train.repeat((n_train, 1))
keys = X_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))
values = Y_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))
net = NWKernelRegression()
loss = nn.MSELoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=0.5)
for epoch in range(100):
trainer.zero_grad()
l = loss(net(x_train, keys, values), y_train)
l.sum().backward()
trainer.step()
print(f'epoch {epoch + 1}, loss {float(l.sum()):.6f}')
keys = x_train.repeat((n_test, 1))
values = y_train.repeat((n_test, 1))
y_hat = net(x_test, keys, values).unsqueeze(1).detach()
# 输出:
epoch 1, loss 211.842209
epoch 2, loss 29.818174
epoch 3, loss 29.818165
epoch 4, loss 29.818157
epoch 5, loss 29.818144
...
其拟合曲线:
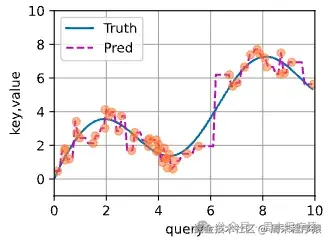
2、多头注意力
前面讲了注意力的参数,目的是通过query结合key,value获取对应的输出,但是如果整个序列只是一个单独的注意力池化,输出的拟合可能不准确,因此加入多头注意力,其公式如下:
其中每个w都是可以学习的参数,这样可以组合多个(query,key,value)获得输出,最后将输出做一层全连接层,得到最终的结果,设计如下:
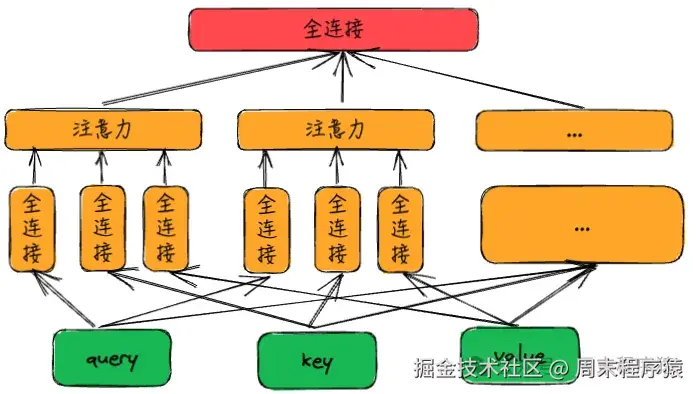
由于大模型的开发中会用到,所以这里给出代码(参考《动手学深度学习》):
def transpose_qkv(X, num_heads):
"""为了多注意力头的并行计算而变换形状"""
# 输入X的形状:(batch_size,查询或者“键-值”对的个数,num_hiddens)
# 输出X的形状:(batch_size,查询或者“键-值”对的个数,num_heads,
# num_hiddens/num_heads)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
# 输出X的形状:(batch_size,num_heads,查询或者“键-值”对的个数,
# num_hiddens/num_heads)
X = X.permute(0, 2, 1, 3)
# 最终输出的形状:(batch_size*num_heads,查询或者“键-值”对的个数,
# num_hiddens/num_heads)
return X.reshape(-1, X.shape[2], X.shape[3])
def transpose_output(X, num_heads):
"""逆转transpose_qkv函数的操作"""
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
return X.reshape(X.shape[0], X.shape[1], -1)
class MultiHeadAttention(nn.Module):
"""多头注意力"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = d2l.DotProductAttention(dropout) # 这里用到缩放点积注意力
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
def forward(self, queries, keys, values, valid_lens):
# queries,keys,values的形状:
# (batch_size,查询或者“键-值”对的个数,num_hiddens)
# valid_lens 的形状:
# (batch_size,)或(batch_size,查询的个数)
# 经过变换后,输出的queries,keys,values 的形状:
# (batch_size*num_heads,查询或者“键-值”对的个数,
# num_hiddens/num_heads)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
if valid_lens is not None:
# 在轴0,将第一项(标量或者矢量)复制num_heads次,
# 然后如此复制第二项,然后诸如此类。
valid_lens = torch.repeat_interleave(
valid_lens, repeats=self.num_heads, dim=0)
# output的形状:(batch_size*num_heads,查询的个数,
# num_hiddens/num_heads)
output = self.attention(queries, keys, values, valid_lens)
# output_concat的形状:(batch_size,查询的个数,num_hiddens)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat)
def attention_nhead():
num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
attention.eval()
batch_size, num_queries = 2, 4
num_kvpairs, valid_lens = 6, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
Y = torch.ones((batch_size, num_kvpairs, num_hiddens))
output = attention(X, Y, Y, valid_lens)
print(output)
attention_nhead()
# 输出:
tensor([[[-3.6907e-01, -1.1405e-04, 3.2671e-01, -1.7356e-01, -8.1225e-01,
-3.7096e-01, 2.7797e-01, -2.6977e-01, -2.5845e-01, -2.3081e-01,
3.0618e-01, 2.7673e-01, -2.6381e-01, -8.4385e-02, 6.8697e-01,
-3.0869e-01, -2.6311e-01, 3.3698e-01, 2.0350e-02, -1.1740e-01,
-2.9579e-01, -2.3887e-01, -1.3595e-01, 1.6481e-01, 3.6974e-01,
-1.2254e-01, -4.8702e-01, -3.3106e-01, 1.9889e-01, 4.6272e-04,
-3.0664e-01, 1.0336e-01, 1.5175e-01, 5.1327e-02, -1.7456e-01,
1.0848e-01, -2.1586e-01, -1.3530e-01, 1.4878e-01, 2.2182e-01,
-1.8205e-01, 4.2394e-02, -1.2869e-01, -6.1095e-02, 1.1372e-01,
-2.4854e-01, 9.8994e-02, -4.2462e-01, -1.9857e-02, -1.0072e-01,
7.6214e-01, 1.4569e-01, 2.4027e-01, -1.4111e-01, -3.5483e-01,
1.2154e-02, -4.0619e-01, -1.7395e-01, 1.2091e-02, 1.2583e-01,
4.5608e-01, -2.2189e-01, 1.1187e-01, -2.2936e-01, 2.6352e-01,
-2.1522e-02, 1.7198e-01, 2.4890e-01, -5.9914e-01, -3.3339e-01,
-5.0526e-03, 2.5246e-01, -5.5496e-02, 8.2241e-02, 2.3885e-01,
-6.4767e-02, 4.5753e-01, 1.4007e-01, 3.2348e-01, -2.9186e-01,
-2.0273e-01, 7.9331e-01, 2.4528e-01, -2.3202e-01, 6.0938e-01,
-3.4037e-01, -3.0914e-01, 2.0632e-01, -1.1952e-01, -1.4625e-01,
5.5157e-01, -1.5517e-01, 5.0877e-01, 1.9026e-01, -3.7252e-02,
-1.7278e-01, -2.9345e-01, -1.2168e-01, 1.7021e-01, 7.7886e-01],
...
不过光看代码,其中每个输入到输出的数据变化,这里不太清晰,于是找资料从网上找到一张解释的图,因此借鉴过来:

3、注意力计算加速库:FlashAttention
我们分析一下以上注意力机制的计算复杂度:
(1)输入长度为n的序列,每个位置进行位置编码有d维的向量,查询矩阵Q的维度为Nxd,键矩阵K的维度为Nxd,值矩阵V的维度为Nxd;
(2)线性变换:对输入的序列进行变换得到Q、K、V,每个token的embedding维度为d,每个都需要计算,复杂度为O(nk3d);
(3)注意力计算:为了获取注意权重,需要对每个序列进行计算,复杂度为O(n^2kd);
(4)最后进行加权求和,复杂度为O(nkd);
总的时间复杂度为O(n^2kd),所以会根据输入的大小成指数增长,为了计算加速,PyTorch2.0以上版本集成FlashAttention。
由于FlashAttention加速原理比较复杂(基于GPU硬件对attention的优化技术),这里原理就不介绍了(后续整理资料再单独介绍),只介绍如何使用:
import torch
from torch import nn
import torch.nn.functional as F
def attention_scaled_dot_product():
device = "cuda" if torch.cuda.is_available() else "cpu"
query, key, value = torch.randn(2, 3, 8, device=device), torch.randn(2, 3, 8, device=device), torch.randn(2, 3, 8, device=device)
output = F.scaled_dot_product_attention(query, key, value)
print(output)
attention_scaled_dot_product()
# 输出如下:
tensor([[[-0.2161, 0.1339, 0.0048, -0.4695, -0.9136, -0.6143, 0.7153,
-0.5775],
[ 0.0440, 0.3198, 0.3169, -0.4145, -0.6033, -0.4155, 0.4611,
-0.3980],
[-0.0162, 0.3195, 0.3146, -0.4202, -0.6638, -0.4621, 0.6024,
-0.4443]],
[[ 0.6024, -0.3102, -0.2522, -1.0542, 0.6863, 0.5142, 1.6795,
0.1051],
[ 0.5328, -0.4506, -0.3581, -1.1292, 1.0069, 0.3114, 1.9865,
-0.0842],
[-1.1632, -1.6378, 0.7211, 1.0084, 0.0335, 1.1377, 1.3419,
-1.2655]]])
参考
(1)阿里云的Notebook:/lab/home?no…
(2)《动手学深度学习》:zh.d2l.ai/chapter_att…
(3)…
